一种基于深度学习的结构拓扑优化方法与流程

本发明涉及建筑桥梁等结构优化设计领域，尤其是涉及一种基于深度学习的结构拓扑优化方法。

背景技术：

人们一直在追寻新颖的设计来提高生产效率，在现代社会，高效的设计方法仍然是一个前景广阔。用最少的材料(成本)来满足使用性能的要求一直是结构设计师们的设计目标，较为传统的方法是基于经验和直觉先做出多种初始设计，然后对每一种方案做计算和分析，并根据结果来决定最终方案，这种方法有很明显的局限性：

首先，初始方案的质量严重依赖设计师的水平；

其次，整个过程需要花费大量的时间和人力成本，并且最优方案可能并不存在于初始方案的集合中。

鉴于传统方法的种种不足，国内外学者开始尝试寻找一种能够基于给定的设计目标自动找出最优设计方案的方法，随着近些年计算机性能的提高以及数学领域优化理论的深入研究，结构拓扑优化技术迅速发展，并在土木、汽车、机械等领域得到了较为广泛的应用。

拓扑优化能够在无初始方案的情况下，基于给定的荷载和边界条件寻找到最符合目标的设计方案，这种方法的优化结果在设计域中可以拥有任何形状、尺寸和拓扑形式，因此具有较高概率找到结构材料利用率最高的结构形式，此外，该方法无需初始设计方案，摆脱了对设计师水平和经验的依赖。

目前已经研究出了许多的拓扑优化方法，可以将它们主要归为以下四类：基于密度的方法、水平集法、进化方法和智能算法。基于密度的方法是目前拓扑优化领域最受欢迎的方法，该方法经过了严谨的数学验证，拥有非常好的稳定性，但是该方法也有其局限性，一方面该方法优化出的最终结果边界上往往包含中间密度单元，需要对结果进行后处理以满足要求；另一方面，该方法得到的结果是局部最优解，而不能保证是全局最优解，水平集法通过更高一维隐函数的边界或等值线来确定结构材料的分部，能够在结构的边界可以创建清晰的界面，而不会出现模糊的现象但由于在数学上的复杂度较高，因此在优化过程中要花费大量的计算时间，进化方法是基于生物进化理论的一种结构优化方法，通过在优化过程中不断删除传力效率最差的一些单元，直到达到预期的体积分数为止，然而该方法在优化初期容易误删某些单元后无法恢复，最终落入局部最优解。

随着计算机科学的发展，智能算法开始被应用于拓扑优化领域，这些算法大多采用仿生学的原理，具有搜索全局最优解的能力，不过相比于其他算法，计算成本过于庞大，无法用来解决实际的工程问题，近几年，由于机器学习算法和计算机芯片(cpu及gpu)计算能力的蓬勃发展，机器学习算法开始逐渐被用来解决拓扑优化问题。目前，这些方法中花费大量时间训练的网络模型泛化能力都相对较差，只能适用于特定的初始条件，不管是采用何种拓扑优化方法，计算效率均是其共同面临的一个问题，尤其是针对大型结构的优化问题。

技术实现要素：

本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种基于深度学习的结构拓扑优化方法。

本发明的目的可以通过以下技术方案来实现：

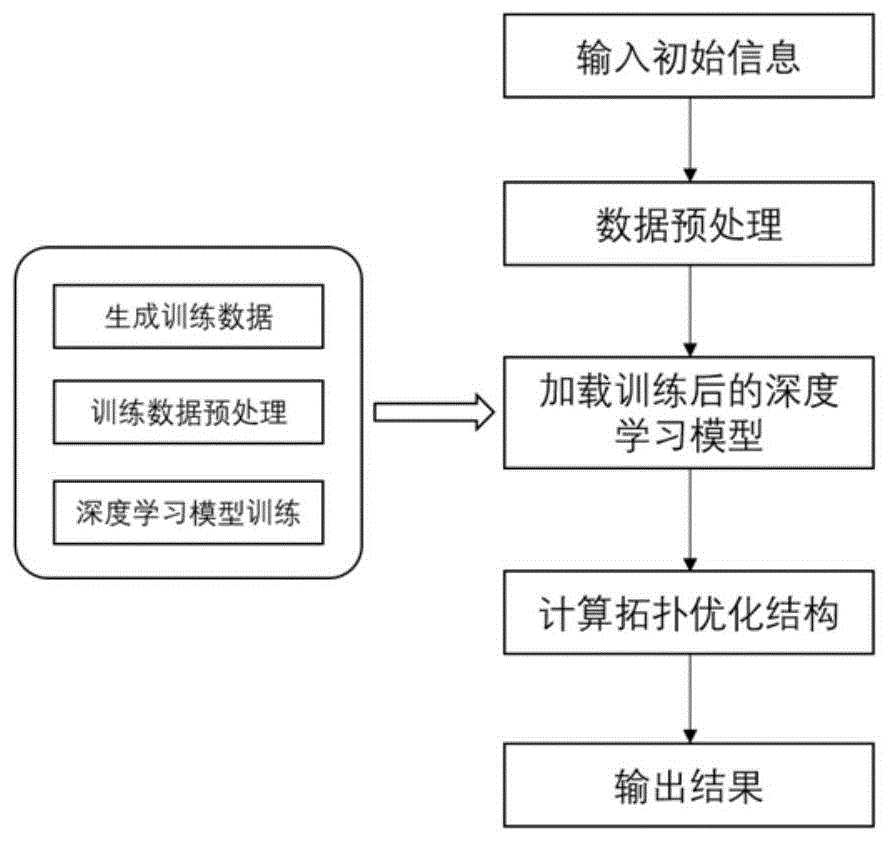
一种基于深度学习的结构拓扑优化方法，包括以下步骤：

1)生成训练数据；

2)对训练数据进行预处理；

3)构建深度学习模型进行训练；

4)采用训练好的深度学习模型进行优化，得到输出结果，即拓扑优化结构。

所述的步骤1)中，训练数据包括设计域尺寸、边界条件、体积分数、惩罚因子、过滤半径、荷载数量和荷载方向。

所述的步骤2)中，预处理后作为深度学习模型的输入张量为一个6通道的输入张量。

该6通道的输入张量具体为：

节点x、y方向的位移作为输入张量的第一个和第二个通道；

节点的正应变εx、εy和切应变γxy作为输入张量的第三个、第四个和第五个通道；

输入张量的最后一个通道的所有数字全部相同且均等于体积分数。

所述的步骤3)中，深度学习模型采用u-net的网络形式。

所述的深度学习模型包括：

编码部分：包括三个连续的编码块，每个编码块内均包含2个卷积层、2个批量正则化层和1个池化层；

解码部分：由多个解码块构成，每个解码块均包含连接层、反卷积层、批量正则化层和卷积层。

所述的编码部分中，最后一个编码块的输出在经历两个额外不同大小卷积核的卷积后进入解码部分。

所述的解码部分中，每个解码块的输入均由两部分组成：一部分来自于前一卷积层，另一部分来自于对应的编码块。

为了使网络输出与二维结构对应，网络的最后一层输出采用一个1通道40*80的张量，最后一次卷积的激活函数采用sigmoid函数，以保证结果对应每一单元最终是否保留的概率。

深度学习模型的训练过程使用的超参数具体为：

训练框架：keras；

l2正则化系数：1e-5；

初始学习率：0.001；

学习率衰减系数：0.1；

学习率衰减条件：连续10轮训练验证集损失不下降；

损失函数：交叉熵；

优化算法：adam。

与现有技术相比，本发明具有以下优点：

一、本发明以机器学习网络模型为核心进行结构的拓扑优化，显著提高了计算效率，本方法仅用传统方法0.38％的时间即可得到基本相同的结果。

二、因为网络本身输入经过精心设计，具有良好的鲁棒性，因此基于本专利提出方法训练的模型具有较强的泛化能力，由悬臂梁边界条件训练的模型可以较好的解决简支梁和连续梁边界条件对应的结构拓扑优化问题。

三、提出了适合解决结构拓扑优化问题的深度学习模型网络结构，实用性强。

附图说明

图1为本发明的方法流程图。

图2为模型输入张量。

图3为网络模型结构。

图4为三种实例的计算结果对比图，其中，图(4a)为常规情况例下传统方法与本发明方法的对比表现，图(4b)为结构断连例下传统方法与本发明方法的对比表现，图(4c)为优于期望例下传统方法与本发明方法的对比表现。

图5为在不同边界条件下传统方法与本发明方法的对比表现，其中，图(5a)为在简支梁边界条件下的表现对比表现，图(5b)为在连续梁边界条件下的表现对比表现。

具体实施方式

下面结合附图和具体实施例对本发明进行详细说明。

实施例

如图1所示，本发明提出一种基于深度学习的结构拓扑优化方法，该方法首先通过传统的变密度法生成大量的训练数据，然后根据设定的规则将原始数据转换为训练数据并以此训练深度学习模型，最后使用训练后的神经网络模型进行高效的结构拓扑优化计算。

关键步骤的具体详细介绍如下：

(1)生成训练数据

通过传统的变密度法生成80000个训练样本，生成训练数据的规则如下表1：

表1生成训练数据规则表

(2)数据预处理

如何将初始信息(设计域尺寸、荷载条件、边界条件)有效的传递给深度学习模型是本方法的关键。通过对比不同输入张量所对应的模型在测试集上的表现，最终确定模型的最佳输入为一个6通道的输入张量，该张量可以将所有的初始信息以一种便于“理解”的方式传递给深度学习模型。如图2所示，输入张量的前两个通道分别对应着节点x、y方向的位移，接下来3个通道表示节点的正应变εx、εy和切应变γxy，最后一个通道的所有数字全部相同且都等于体积分数要求。

(3)深度学习模型训练

针对结构拓扑优化问题，表现最佳的网络模型结构如图3所示，采用u-net的整体框架结构，整个神经网络总体采用u-net的网络形式，主要分为两部分：

1)编码部分：将输入的数组下采样，返回一个维数下降的数组。

2)解码部分：将输入的数组上采样，返回一个维数上升的数组。

考虑到输入的节点信息尺寸为41×81，而输出的单元分布信息尺寸为40×80。因此将输入张量正式传入编码部分前，需要先经过一次卷积，将其调整为40×80，便于u-net的连接。随后输入张量通过三个连续的编码块(encodingblock)，其中每个编码块内包含2个卷积层、2个批量正则化层和1个池化层。最后一个编码块的输出在经历两个额外不同大小卷积核的卷积后进入解码部分。

每个解码块(decodingblock)都包含连接层，反卷积层，批量正则化层和卷积层。与编码块不同的是，每个解码块的输入都由两部分组成：一部分来自于前一卷积层，另一部分来自于对应的编码块，这也是u-net网络最大的特点。为了使网络的输出与二维结构对应，网络的最后一层输出为一个1通道40×80的张量，其中最后一次卷积的激活函数采用sigmoid函数，以保证结果对应每一单元最终是否保留的概率。

模型训练过程使用的全部超参数如表2所示。

表2模型训练超参数表

本发明以机器学习网络模型为核心进行结构的拓扑优化，显著提高了计算效率，与传统方法相比计算时间对比见表3，随机挑选结算结果对比见图4，本专利提出的方法仅用传统方法0.38％的时间即可得到基本相同的结果。

表3单个样本所需计算时间统计表

因为网络本身输入经过设计，具有良好的鲁棒性，因此基于本专利提出方法训练的模型具有较强的泛化能力，由悬臂梁边界条件训练的模型可以较好的解决简支梁和连续梁边界条件对应的结构拓扑优化问题，如图5所示。