上一篇我们已经介绍了,基于最小势能原理的单元平衡方程是有限元计算的根本。其形式就是单元刚度矩阵(element stiffness matrix)乘以位移向量等于右边的荷载向量(right hand side vector):
其中, 为单元刚度矩阵。
为右侧的单元荷载向量。
这里的是体积的微分,在二维问题里,写开来其实就是
(所以
当然是
啦)。 进一步放到母单元中可以写成
,那么
,右边的荷载向量也可以用Jacobian矩阵做mapping,然后积分。以上内容在上一篇已经讲得十分完备了,这里复读了一遍。
那么问题来了,这个刚度矩阵和荷载向量的积分要怎么算?譬如荷载的积分,我们知道,一个四边形单元(quadrilateral element)的每个点在两个方向上都有应力分布,而且考虑到实际情况,这个应力往往是一条曲线!譬如我们对着母单元这样横着切一刀,我作为好事者想看看这个截面上的竖直方向的正应力如何?
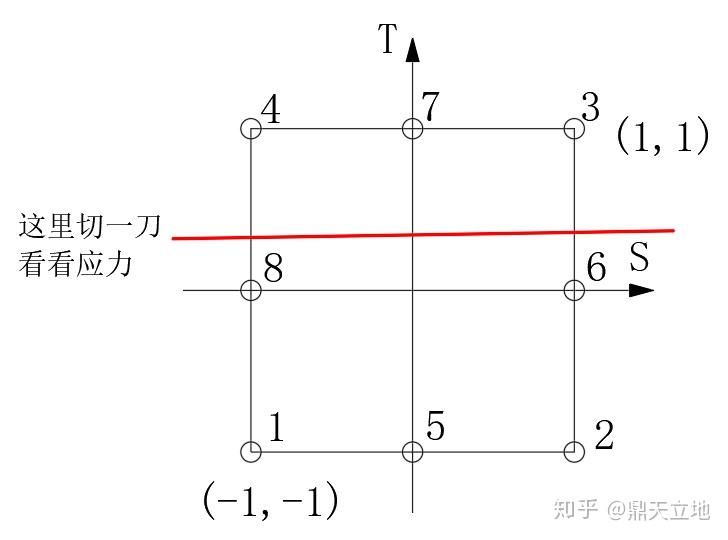
有同学可能要问为什么我要横着切一刀?为什么不是斜地切一刀……因为斜着切一刀的图像其实就是横切与竖切的图像合成,所以我们先横着切一刀看看。
然后你会发现正应力分布图是这货(略夸张,其实没那么弯曲):
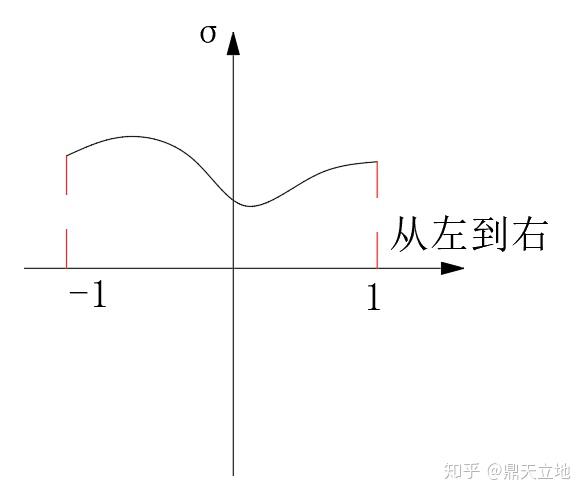
没错,除了重力这种均匀分布的简单力之外,其他的应力分布基本都是变化的一条曲线!考虑到我们要把荷载整合到单元结点上面去,我们必须算出积分(合力)的结果!算积分就是算面积呗,这是大学生常识。但是要是每个单元都通过算面积的办法来算积分的话,几百上千个单元的时候会消耗计算机大量算力,结果也不保证精准。
计算机算微积分是很耗资源的行为。(可以拿着你手里的991计算器算个微积分,能有直观感受。)
于是高斯积分方法就呼之欲出了!
高斯积分法的原理其实很简单,我们要对一个函数在 区间内求积分,即
,在我们有限元里就是其数值解可以通过某几个点的函数值加权来确定,用算式写出来就是:
这里的 就是各个函数值的权重,n是高斯积分点的个数,
是各个高斯积分点的函数值。下面我们结合例子来解释一下这三样东西(教材里直接丢出来这个公式完全看不懂啊)。
我们先从最简单的函数,线性函数开始。譬如在 内是一根直线,如图所示:
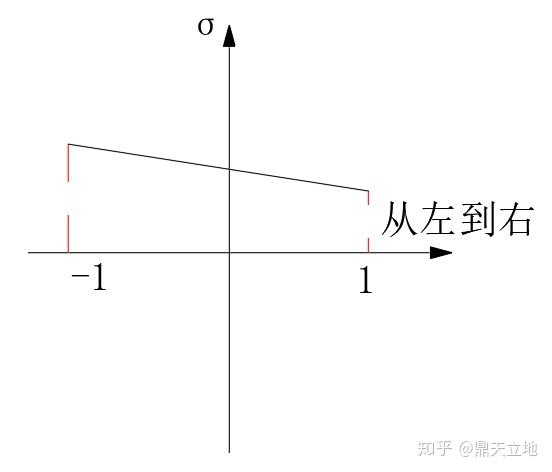
那么显然,该积分就是梯形的面积,当然是上底加下底乘高除以二(小学生水平)啦。同时我们发现这里的面积还可以这么算: ,这里高斯积分点在中间
的位置,确定的权重是2,积分点的函数值是
那么假如是二次式呢? 怎么办?拿出草稿本计算一下发现:
也是相当简单,我们忽然“发现”它可以写成
那我们就可以假设需要两个高斯积分点,权重各为1,高斯积分点在左右两边 的地方。
换句话说,对于线性函数,只要你告诉我,我无需知道函数式,就可以算出你的积分(面积)了!对于二次函数,只要你告诉我
这俩函数值,我既不需要知道函数的表达式,更不需要做积分计算,只要把这俩函数值各乘以权重(大小都为1)相加即可算出积分值了!
好开心啊,那么我们来看看三次函数: ,居然也满足
那显然,其高斯积分点位置和权重跟二次曲线一样的嘛!所以接下来算四次曲线和五次曲线同样能得到相似的结论:四次曲线有三个高斯积分点,分别是0(权重为 )和
(权重均为
),五次曲线与四次曲线一致。
六次曲线和七次曲线则需要四个高斯积分点,规律也是一样的。也就是说,n个高斯积分点可以应付2n-1次及以下的曲线积分。
现在有一条七次曲线摆在我眼前,我不需要知道它的函数式就能算出积分:
其中 为四个高斯积分点的权重,
是四个高斯积分点的位置,具体数字查书吧——根号套的有点多我从来没记住过。
算了还是写一下吧,送佛到西天。
其中两个积分点:
权重均为
另外两个积分点
权重均为
在绝大多数情况下,用五次曲线去模拟应力分布绰绰有余了。因而只要用三个高斯积分点就够了(只用两个的话只能对付三次曲线,精度上还有些吃力)。只要在母单元每个方向上面布置三个高斯积分点就可以获得精确的五次函数曲线的积分。当然你要是研究复杂的等参变换,就当我没说。
那么什么叫”每个方向都布置三个高斯积分点“?
譬如要算竖直方向的积分,我一开始以为是这样的(智障):
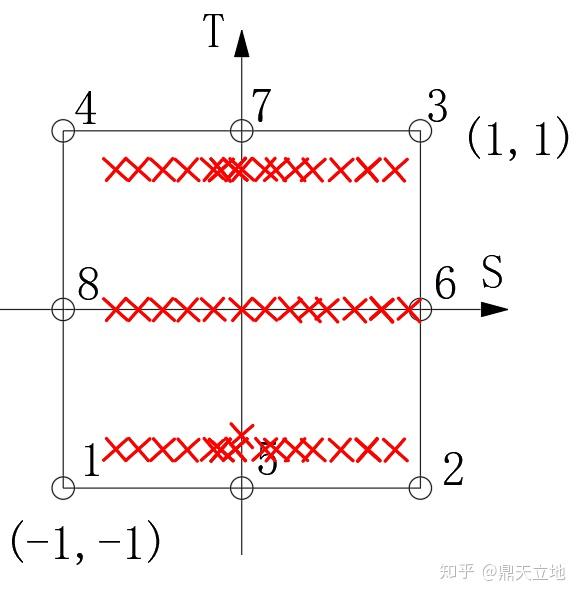
水平方向的积分,我一开始以为高斯积分点应该是这样的(智障X2):
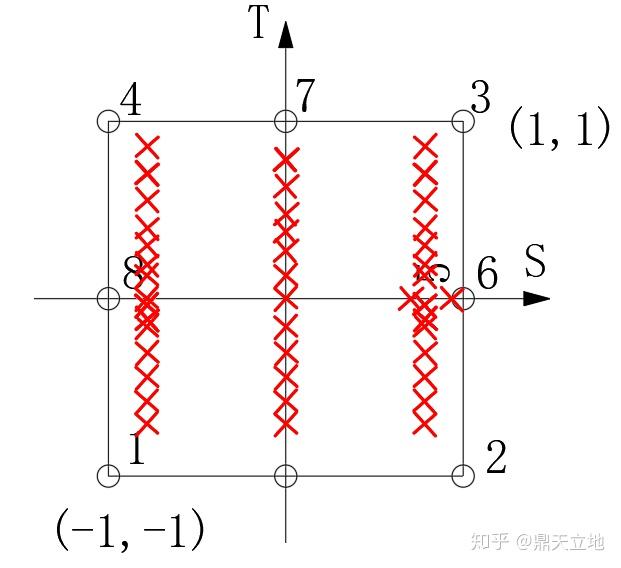
但是实际上,我们有限元应用里,高斯点是这样的:
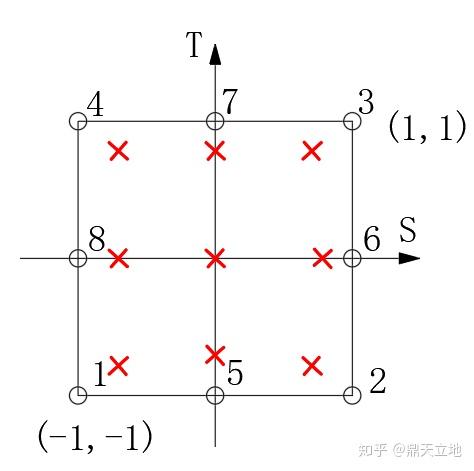
只要画九个就行了啊!正好每个方向都有三个,横坐标和纵坐标为0(权重为 )和
(约0.77,权重均为
)。第一个布置高斯点的人真是个天才。
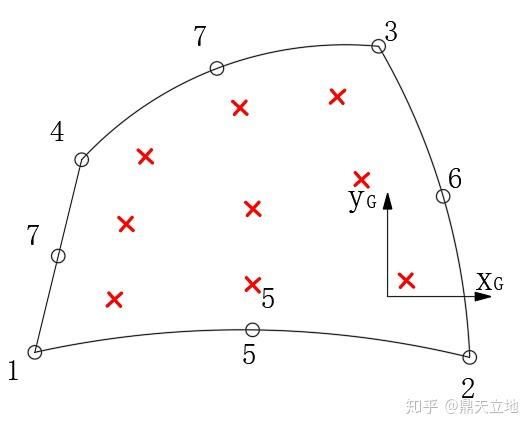
因而,计算机在计算应力积分的时候,只要把这九个点的数据揪出来,就可以算出五次函数曲线的积分值了。也就算出了该单元的荷载向量!单元刚度矩阵的积分同理。所以许多有限元程序会输出单元的应力应变值,往往是高斯积分点的函数值(不要以为是结点的!)
Q&A:
问:那假如我想知道某一个结点的应力值怎么办?
答:计算机会用算法寻找到其附近的几个高斯点然后做插值计算。
问:你这里展示的是3x3的高斯点,那我可不可以用2x2的?
答:假如你是四结点单元的话,当然可以使用,精度还行;如果是八结点单元,用2X2(四个高斯点)会有误差。
问:你这里展示的是平面四边形单元高斯积分点布置,那么假如是三维情况(六面体单元)怎么布置啊?
答:平面是2x2的话,对应的六面体就是2x2x2共八个点;平面是3x3的话,六面体就是3
x3x3共27个高斯点,具体怎么布置请自行脑补。
问:你这里高斯点是用在四边形单元上,那么三角形单元有高斯积分点吗?
答:三角形单元用普通的数值积分,不用高斯积分点。三角形单元的数值积分形式可以自行查阅,比高斯积分要简单。